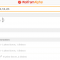
What mark do you need to get the desired average?

What mark do you need to get the desired average? In detail, let us consider a student who up to date received in a discipline the following sequence of marks

Moreover, let us assume that in his school, the marks to be listed in the official documents, must be integers ranging from 1 to 10. In this case, the teacher calculates the average of the marks and then rounds to the greatest integer lower to the average (called floor) or for excess to the lowest integer greater to the average (called ceil), depending on the average is closer to the integer that proceeds or to the next one. Usually, if the average is equal exactly to the average of two consecutive integers, one chooses the ceiling as the final mark.

Till now, we talked about the average of the marks, but we did not know how this average is calculated. It is calculated as a simple arithmetic mean, that in our context is the sum of the sequence of marks divided by their number in the sequence

Let us suppose that the student, not satisfied with the average of his marks, asks his teacher for an additional exam to eventually improve his average. At this point, it is fundamental that the student asks himself what is the minimum mark v that he should get in the next and last exam to obtain the desired final mark t. For all that, we told above, the student should change the old average to

that anyway, should not be lower to t – 1/2:

The last mathematical expression is an inequality of the first degree, easily solvable with respect to v. It is straightforward to prove that its solution is

This hand right side of the inequality provides an expression of the minimum mark that the student should get to obtain the desired mark t. Of course, it is not rare that for such students the solution to this problem gives v greater than 10. This result means that the student could not obtain the desired final mark and he should settle on his old average eventually rounded to the ceil. However, in the case of v not greater than 10, it could happen that the student could not obtain v as the last mark, or worse he could receive a vote much lower than v that will bring his average lower by at least one unit with respect to the previous one.

I think that this simple application of the first degree inequalities should be known to teachers and students, because in many cases, students try to improve their marks average by spending their time (and that of their teacher) without success, just because they started to study the discipline very late, after to have collected a long sequence of low marks.

Then, what is the solution to the problem for the student? The solution could be to monitor continuously the average of the marks, by using the inequality here introduced to make a decision process on the minimum mark that the student needs to maintain their average or increase it. If this work is done from the start of the school period till the end, this method could give positive results. Of course, the students should not forget the main cause of their success: continuous and serious study without interruptions!