Fractions LCM: Mathway vs WolframAlpha

What is the Least Common Multiple (LCM) of two or more fractions? Probably, one can ask himself “What do I need this calculation for?” or maybe one thinks that it is equal to the LCM between the denominators of the fractions.

The answer is that it is wrong to confuse the LCM of more fractions with that of their denominators. In fact, if we consider the following three fractions

\(\displaystyle \frac{1}{2}, \frac{1}{3}, \frac{2}{3}\),

the majority of people will identify their LCM with the number \(6\) because of LCM between their denominators. However, the correct answer is \(2\).

Before providing an exhaustive explanation of this result, we will discuss an important application of LCM between fractions.

What is the period of the linear combination of periodic functions?

Let \(\alpha\) and \(\beta\) be a non-zero real numbers, \(f\left(x\right)\) and \(g\left(x\right)\) be periodic functions having periods \(T_f\) and \(T_g\). Is the linear combination \(\alpha f\left(x\right)+\beta g\left(x\right)\) of the two functions periodic? If yes, what is its period?

Answer: If the periods \(T_f\) and \(T_g\) are commensurable, then the function \(h\left(x\right)=\alpha f\left(x\right)+\beta g\left(x\right)\) is periodic and its period is equal to the LCM of \(T_f\) and \(T_g\). In symbols: \(T_h=LCM\left(T_f, T_g\right)\).

To give an example, let us consider the following linear combination of periodic functions

\(\alpha \sin{\left(4\pi x\right)}+\beta \sin{\left(6\pi x\right)}+\gamma \sin{\left(3\pi x\right)}\).

Since the minimum period of the sin function is \(2\pi\), it is straightforward to see that those of the three functions are, respectively, \(\displaystyle \frac{1}{2}, \frac{1}{3}, \frac{2}{3}\). The latter ones are exactly the fractions that we have considered in the introduction of this article. Let us see to understand why their LCM is equal to \(2\).

LCM algorithms: Mathway vs WolframAlpha

Mathway

Let us choose to use two popular apps for mathematics: Mathway and WolframAlpha.

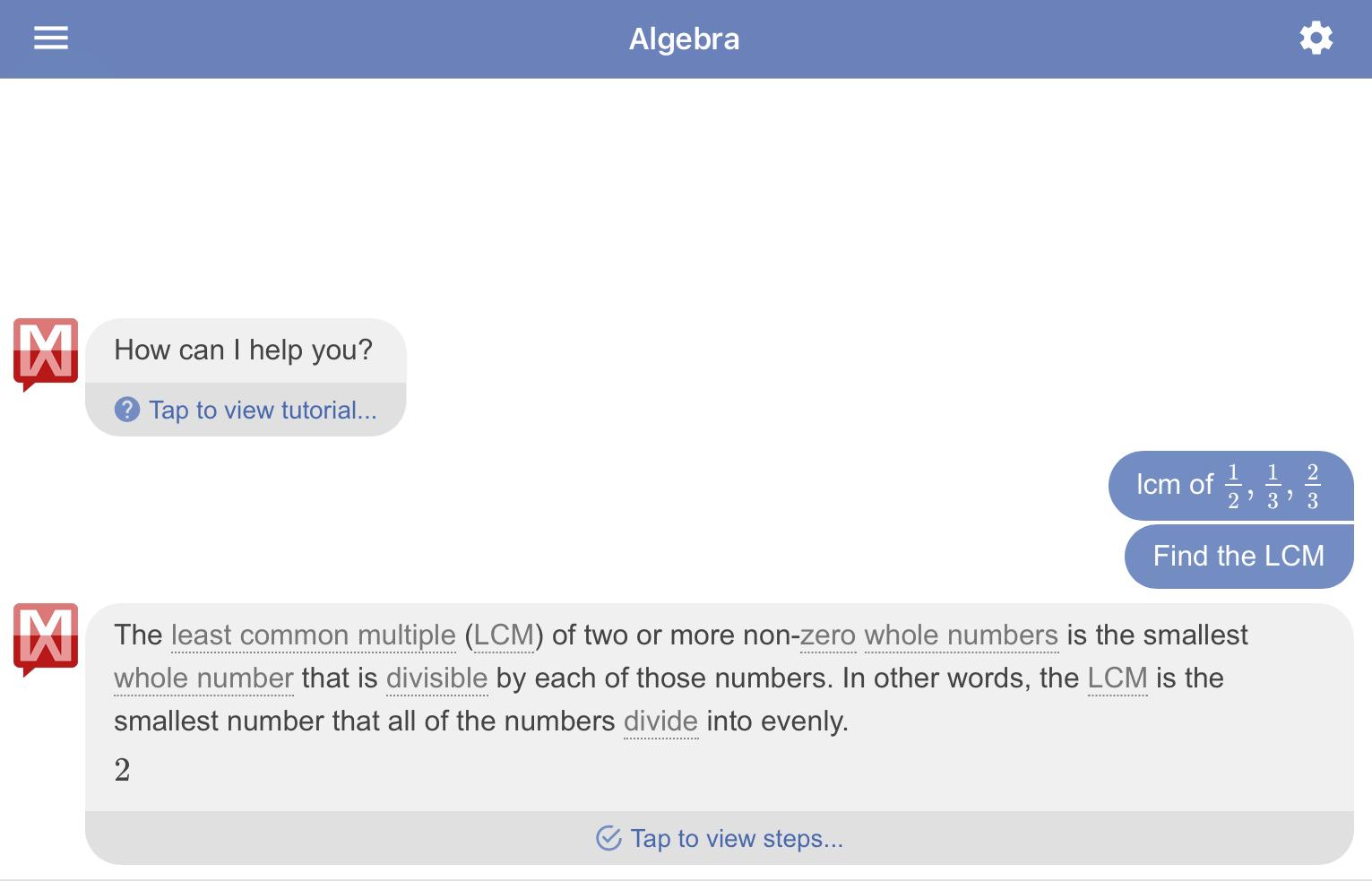
In the Mathway app, to obtain the result of LCM of \(\displaystyle \frac{1}{2}, \frac{1}{3}, \frac{2}{3}\), it will be sufficient to write in the text field the following string:

 lcm of \(\frac{1}{2}, \frac{1}{3}, \frac{2}{3}\).

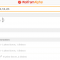
Consequently, the software will recognize what problem we are asking to solve. In such a case “Find the LCM” and it will provide its solution immediately below (see figure below).

It is remarkable to see that Mathway remembers the definition of LCM of two or more non-zero whole numbers, and not that between fractions. Really, in such a definition of LCM, it is not necessary to specify the kind of numbers we are considering, because it is rather general. Mathway, in doing so, it would seem that wrongly applies the LCM algorithm for the whole numbers to the fractions. Luckily, it is not so! In fact, by clicking on “Tap to view steps…”, it is possible to go read the algorithm really used, and here is shown in the figure.

Without going into too much detail, the algorithm used by Mathway for finding the LCM between fractions consists of the next two steps:

WolframAlpha

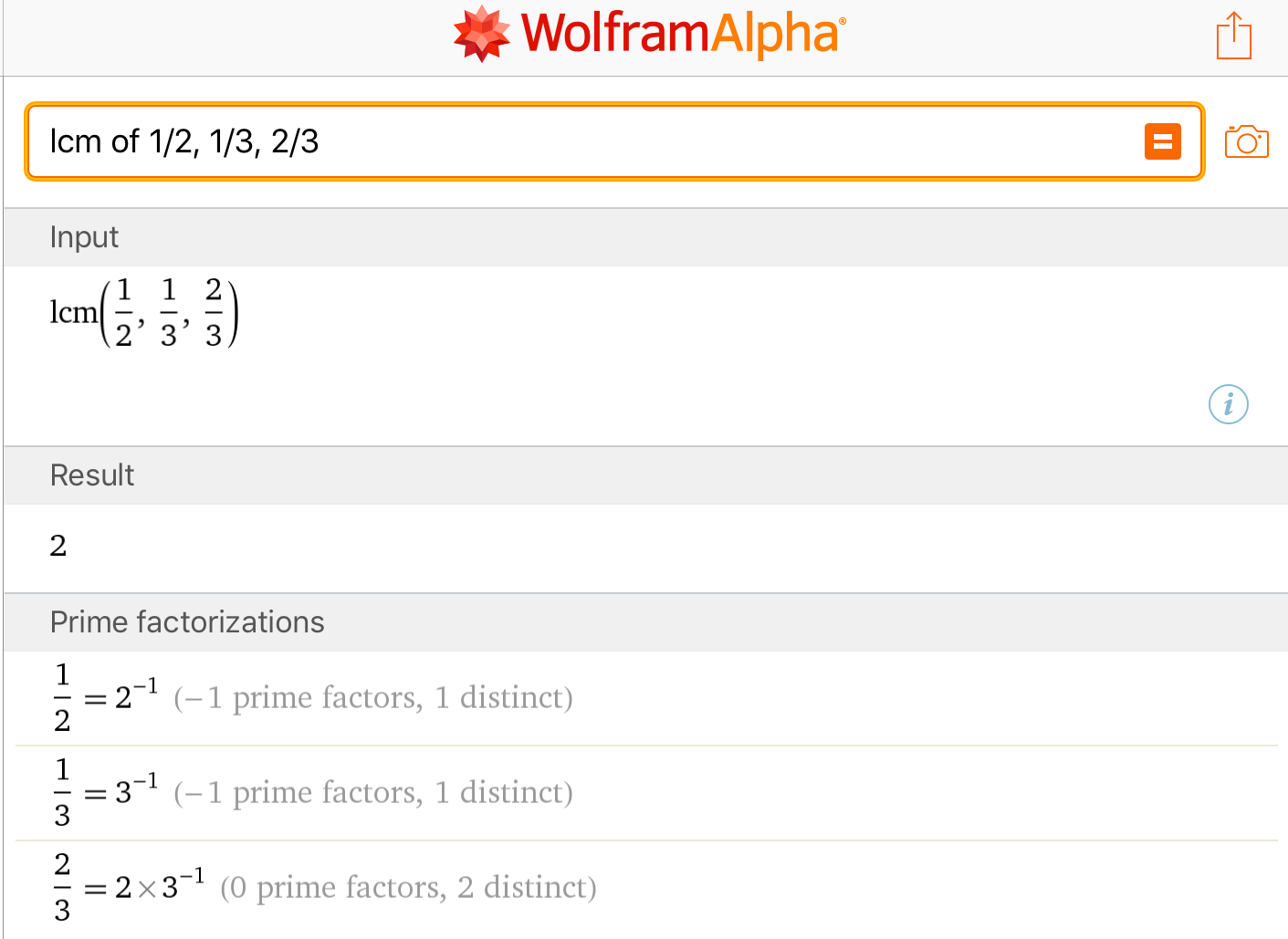
Now, let us use WolframAlpha. To obtain the result of \(\displaystyle \frac{1}{2}, \frac{1}{3}, \frac{2}{3}\), we write in the text field the string:

 lcm of 1/2, 1/3, 2/3

Once again the result is \(2\), confirming that the algorithms used by the two apps are equivalent. Let us analyze what is the algorithm used by WolframAlpha.

As it is possible to see in the figure below, WolframAlpha factorizes the three fractions in prime factors, but it is not very clear what it does next. Let us see it together, by writing here the prime factorizations of the three fractions

\(LCM\left(\frac{1}{2}; \frac{1}{3}; \frac{2}{3}\right)=LCM\left(2^{-1}; 3^{-1}; 2^1\cdot 3^{-1}\right)\).

Now, remembering that the LCM between numbers is equal to the product of the highest power of each prime number together, we get

\(LCM\left(2^{-1}; 3^{-1}; 2^1\cdot 3^{-1}\right)=LCM\left(2^{-1}\cdot 3^0; 2^0\cdot 3^{-1}; 2^1\cdot 3^{-1}\right)=2^1\cdot 3^0=2\),

where we have completed each factorization with powers at zero exponents, in a way that each fraction is expressed by the same number of powers of the prime numbers appearing in the original factorization.

Lastly, since the two LCM algorithms between fractions, here discussed, are not unique existent ones, we will reserve to discuss some other one in a future post.

---

©Stefano Spezia. This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.