Solved problem: a ball moving around a vertical circumference

Solved problem

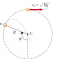
A ball is tied to one end of a string. The other end of the string is held fixed. The ball is set moving around a vertical circumference without friction, and with speed \(v_i=\sqrt{Rg}\) at the top of the circumference, as in the figure below. At what angle \(\theta\) should the string be cut so that the ball will then travel through the center of the circumference?

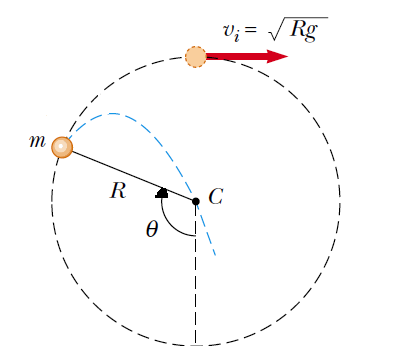
Solution

With the aim to give an answer to the problem, we need to find out at what angle \(\theta\) the tangential velocity, such that the ball on release from centripetal force from tension in the string, has the correct horizontal and vertical components to give rise, in its subsequent free-fall motion, the correct parabolic trajectory that enables the ball to pass through the center.

Since the ball is kept moving around the vertical circumference, with a minimum speed at the top such that the string tension is null, firstly, it is necessary to find how the ball speed \(v_0\) varies with the angle \(\theta\). Since all the forces within the system are conservative, it is possible to utilize the principle of the conservation of mechanical energy, which states that the total mechanical energy in a system remains constant as long as the only forces acting are conservative. Remembering that the total mechanical energy is given by the sum of the potential energies and those kinetic ones, we have the following equation

\(\displaystyle\frac{1}{2}mv_i^2+mgR\left(1+\cos{\theta}\right)=\frac{1}{2}mv_0^2\left(\theta\right)\),

that solved for the speed \(v_0\left(\theta\right)\) gives

\(v_0\left(\theta\right)=\sqrt{\left(3+2\cos\theta\right)gR}\).

Now, it is convenient to write down the parametric equations of the parabolic trajectory of the ball after the string is cut. By setting a system of Cartesian axes at the center of the circumference and \(t=0\) as the time instant when the string is cut, we get

\(\displaystyle\begin{cases} x\left(t\right)=-R\sin\alpha+v_0\left(\theta\right)t\cos\alpha \\ \displaystyle y\left(t\right)=R\cos\alpha+v_0\left(\theta\right)t\sin\alpha-\frac{1}{2}gt^2\end{cases}\),

where we have been set \(\alpha=180^{\circ}-\theta\).

By setting \(x\left(t\right)=y\left(t\right)=0\), from the first equation of the latter system, we can derive the expression of the time instant \(t\) when the ball travels through the center of the circumference, and substitute it into the second equation. After some simplification, the latter one reads

\(2v_0\left(\theta\right)-gR\tan^2\alpha\cos\alpha=0\).

Now, replacing \(v_0\left(\theta\right)\) with \(\sqrt{\left(3+2\cos\theta\right)gR}\), using the goniometric identity

\(\displaystyle \tan^2\alpha=\frac{1-\cos^2\alpha}{\cos^2\alpha}\)

and the supplementary angle identity \(\cos\alpha=\cos\left(180^{\circ}-\theta\right)=-\cos\theta\), we find

\(\displaystyle 3+2\cos\theta+\frac{1-\cos^2\theta}{\cos\theta}=0\).

This latter one is a quadratic goniometric equation

\(\cos^2\theta+3\cos\theta+1=0\)

whose only real solution is

\(\displaystyle \theta=\cos^{-1}\frac{\sqrt{5}-3}{2}=112^{\circ},5\)

In conclusion, the string should be cut at the angle \(\theta=112^{\circ},5\) so that the ball will then travel through the center of the circumference.

References

OEIS Foundation Inc. (2022), Entry A132338 in The On-Line Encyclopedia of Integer Sequences, http://oeis.org/A132338

©Stefano Spezia. This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.