Minimum speed to throw down a parallelepiped
Problem text
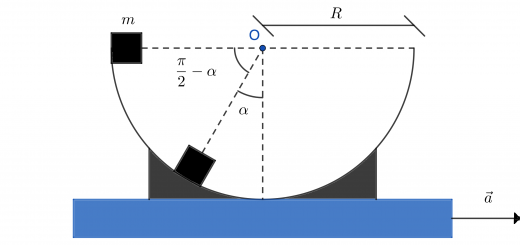
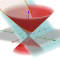
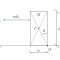
Let us consider an object shaped as a parallelepiped and placed on a horizontal plane with friction (see figure). In particular, let us suppose that the object has a mass \(M\), a width \(w\) and a height \(h\). Now, let us imagine to throw a ball having mass \(m\) at speed \(v_0\) against the object, and at a height \(d\) lower than \(h\).
At what minimum speed \(v_0\) does the ball throw down the object whereas the impact is elastic?
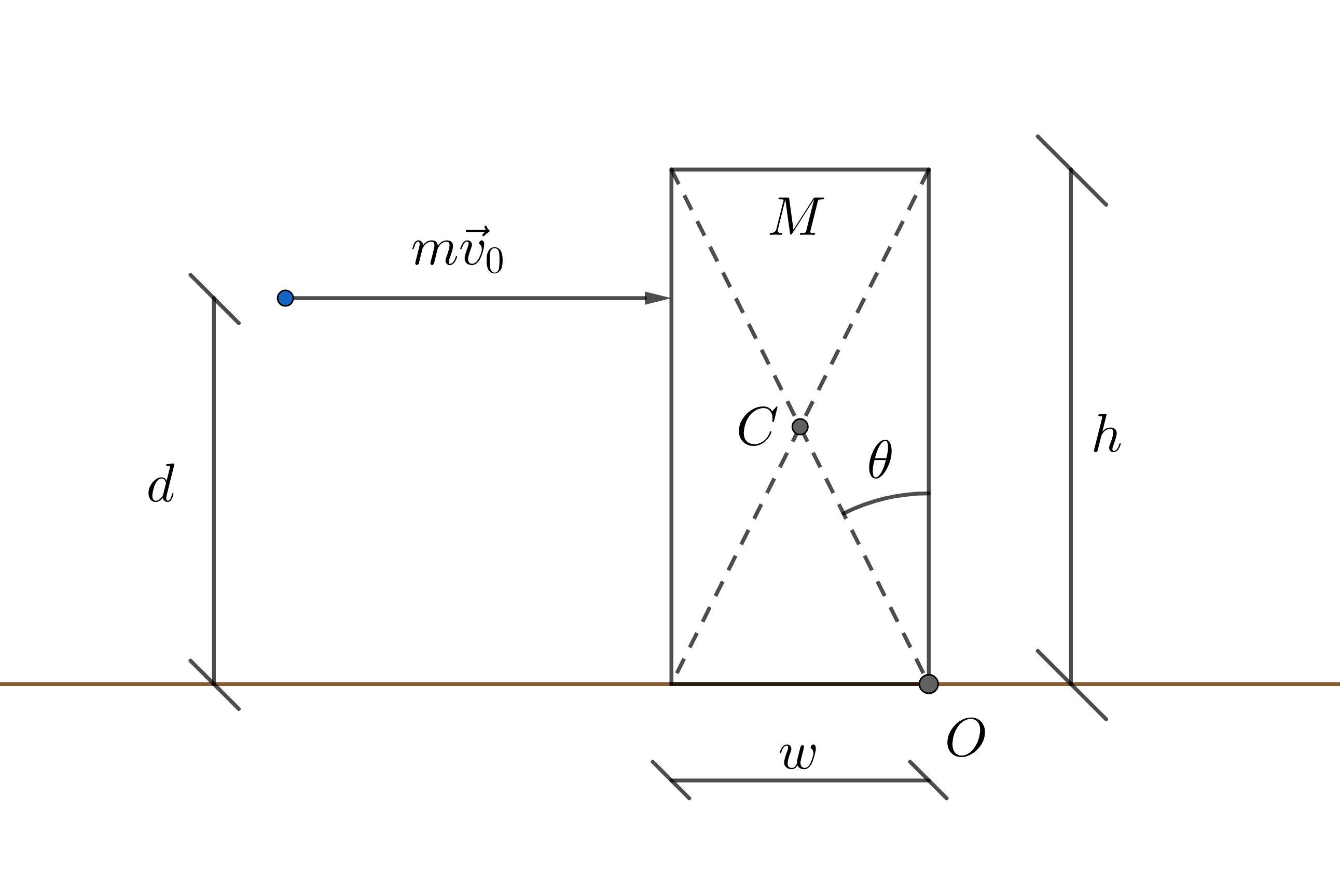
In order to answer the question, we need to understand how the impact affects the motion state of both the objects.
Principles of conservation in an elastic collision
For simplicity, we hypothesize that the friction coefficient of the horizontal plane is sufficiently high to avoid any translation of the bumped object. Moreover, we suppose that the velocity \(\vec{v_0}\) is parallel to the plane. In these conditions, we define with \(I\), \(\omega_f \) and \(v_f\), respectively, the moment of inertia of the object with respect to an axis passing through point \(O\) and perpendicularly to the sketch, its angular speed just an instant after the impact, and the ball speed even immediately after the collision.
Having considered the impact be elastic, it is possible to use the principle of conservation of both the mechanical energy and of the angular momentum
\(\begin{cases}\displaystyle \frac{1}{2}mv_0^2=\frac{1}{2}I\omega_f^2+\frac{1}{2}mv_f^2 \\ mv_0d=-mv_fd+I\omega_f \end{cases}\).
The latter one is a system of two quadratic equations. It can be easily solved by rewriting it in the following way
\(\begin{cases}\displaystyle m\left(v_0^2-v_f^2\right)=I\omega_f^2 \\ md\left(v_0+v_f\right)=I\omega_f \end{cases}\).
In fact, dividing each other both sides of the two equations, remembering the remarkable product “Addition multiplied by subtraction” \(v_0^2-v_f^2=\left(v_0+v_f\right)\cdot \left(v_0-v_f\right)\), it is straightforward to obtain
\(\begin{cases}\displaystyle \omega_f=\frac{2v_0}{d+\frac{I}{md}} \\ \displaystyle v_f=v_0\frac{I-md^2}{I+md^2} \end{cases}\).
Mechanical energy conservation after the impact
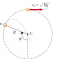
Now, in order to find the relationship existing between \(\omega_f\) and the maximum angle of rotation \(\alpha\) of the parallelepiped without the latter one to fall down, we use again the conservation principle of the mechanical energy
\(\displaystyle \frac{1}{2}I\omega_f^2=Mg\sqrt{\frac{w^2+h^2}{4}}\left(1-\cos{\alpha}\right)\).
Here, we have utilized the expression
\(\displaystyle \sqrt{\frac{w^2+h^2}{4}}\)
equal to the distance between the centroid \(C\) and the point \(O\).
Since the rotation angle necessary to induce the fall of the parallelepiped is equal to the angle
\(\displaystyle \theta=\tan^{-1}\frac{w}{h}\),
we set \(\displaystyle \alpha=\theta\).
Before to continue with the next algebraic manipulations, let us express the momentum of inertia \(I\) of the parallelepiped as a function of \(w\), \(h\) and \(M\). In detail, considering that the inertia momentum with respect to the axis perpendicular to the sketch and passing throw the centroid \(C\) is
\(\displaystyle I_0=M\frac{w^2+h^2}{12}\),
and applying the Huygens–Steiner theorem, we get
\(\displaystyle I=I_0+M\frac{w^2+h^2}{4}=M\frac{w^2+h^2}{3}\).
Algebraic manipulations
In the end, it is necessary:
- to replace:
- the expression of the momentum of inertia \(I\) into both the expression of \(\omega_f\) and the last equation of conservation of the mechanical energy;
- the expression of \(\omega_f\) into the mechanical energy conservation equation;
- \(\alpha\) with \(\displaystyle \tan^{-1}{\frac{w}{h}}\);
- to use the goniometric identity \(\displaystyle \cos{\phi}=\frac{1}{\sqrt{1+\tan^2{\phi}}}\);
- to isolate \(v_0\).
At the end of the operations listed above, one gets
\(\displaystyle v_0=\left[d+\frac{M\left(w^2+h^2\right)}{3md}\right]\sqrt{\frac{3gw}{4\left(w^2+h^2\right)}}\).
Therefore, in order to throw down the object with the shape of a parallelepiped, the ball of mass \(m\) must be thrown against it with a speed \(v\) at least higher than \(v_0\):
\(\displaystyle v>\left[d+\frac{M\left(w^2+h^2\right)}{3md}\right]\sqrt{\frac{3gw}{4\left(w^2+h^2\right)}}\).
©Stefano Spezia. This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.