What is the Cartesian equation of a round cartoons cloud?
What is the Cartesian equation of a round cartoon cloud? What do we mean by a cartoon cloud? Of course, I do not mean a real cloud made by water steam, and floating in the sky, but those clouds are often used in cartoons. For the sake of mathematical simplicity, in this post, we assume the restriction that such a cloud is round.
For obvious reasons, this kind of cloud has a center of symmetry, and being a closed curve must be inscribed by a circle. This last one is a figure of the plane geometry and its mathematical proprieties are enough reported in math textbooks. As we know, the Cartesian equation of a generic circle is:
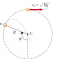
where x0 and y0 are the cartesian coordinates of the center, and r is the radius. Let us make a graphical example. By setting x0, y0, and r equal respectively to 3, 4, and 2, we have the following graphics by GeoGebra.

In geometry, it is also possible to describe a curve by using different kinds of equations. They are parametric equations and have the characteristics to define the coordinates of the points that make up a geometric object as functions of one or more independent variables, called parameters. In such cases, the equations give the parametric representations of the object.
By coming back to our example of a circle, we can define the following set of equations

where t is the unique parameter.
It is just from this set of equations, that we can easily build a round cartoon cloud. To reach our aim, we can draw an integer number of smaller semicircles on the circle, by modulating (varying) the radius of the circle. To get that, we can add a sin function to the radius r, but we have to remember that so doing, we do not get the desired cloud. If we replace r with
in the parametric representation, we obtain a curve that is not inscribed by the initial circle. Moreover, at the coordinates (5, 4) the curve shows a sharp corner. Here in the example, h e k
are equal to 0.5 and 6.5 respectively.

To solve these two problems, it is possible to change the modulation of the radius with the following expression
In such case, we obtain a round cartoons cloud.

By hiding the objects used for its construction, we have the following figure.
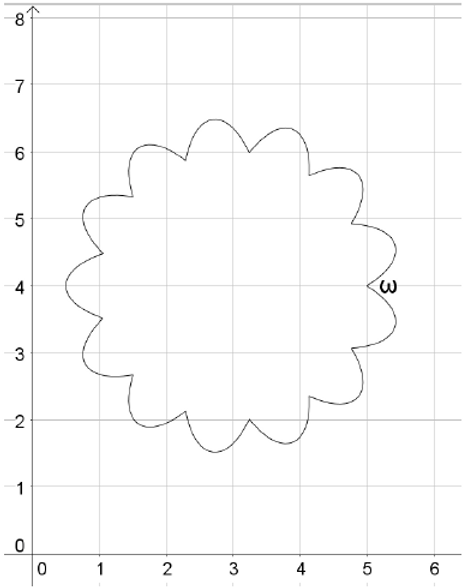
We have reached our goal of drawing a round cartoon cloud using its parametric representation;
despite that, we did not consider some issues:
1. What do the quantities h and k represent?
2. What numerical sets h and k belong in?
3. Is it possible to obtain a Cartesian representation of this curve?
Let us discuss the first issue. The quantities h and k are two constants, and no parameters, and represent respectively the amplitude of the sinusoidal modulation of the radius ℎ = 0.5 and the number of periods of the sin function contained over a complete round, and divided by two (13/2 = 6.5).
From the meanings of the quantities h and k, we can understand that h can assume any real and positive value lower than r, while k must be a semi-integer, having 2k to be an even number.
By moving to the last issue, we must see if we can derive the Cartesian equation of such a curve from its parametric representation. The answer is positive!
By rewriting the set of parametric equations in the following way,

squaring and adding them side by side, we obtain

The last equation does not yet represent a Cartesian equation because the parameter t still appears on the right-hand side.
It is straightforward to see that the t must be equal to

and so, the desired Cartesian equation be the following: